Na rozdíl od rezistorů závisí reaktance kondenzátorů (kapacitorů) a cívek (induktorů) na kmitočtu. Kombinací těchto prvků můžeme vytvořit obvody (dvojbrany), jejichž přenos je závislý na frekvenci.

Definice pojmů

Reaktance je imaginární částí impedance součástky. Reaktance indukčního charakteru se nazývá induktance, reaktance kapacitního charakteru je kapacitance a vypočítá se ze vztahu:

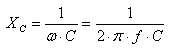
Dvojbran (čtyřpól) je libovolný obvod, který je s jinými částmi obvodu spojen dvěma páry svorek (vstupní a výstupní svorky).

Napěťový přenos je vyjádřen jako poměr výstupního napětí ke vstupnímu. Je-li přenos větší než 1, jedná se o zesílení, v opačné případě jde o útlum.

Napěťový přenos se obvykle vyjadřuje v decibelech:

Dolní propust (integrační článek RC a RL)

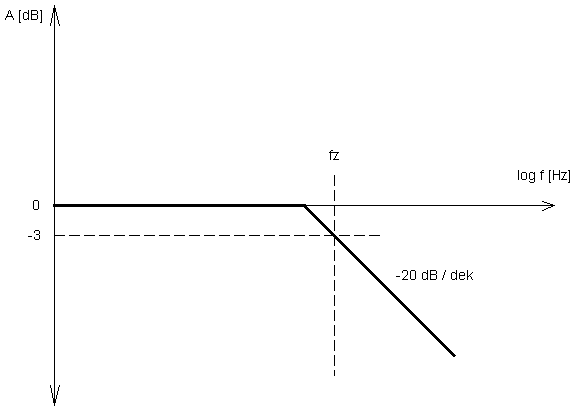
Integrační článek má frekvenční charakteristiku dolnopropustného filtru – se zvyšující se frekvencí vstupního napětí výstupní napětí klesá. U ideálního integrátoru odpovídá desetinásobnému zvýšení frekvence desetinásobný pokles amplitudy, sklon jeho logaritmické amplitudové frekvenční charakteristiky tedy je −20 dB/dek.

Přenos napětí pro integrační článek RC se vypočítá ze vztahu:

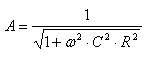
kde ω je kruhová frekvence střídavého proudu (2π.f), C kapacita kondenzátoru a R ohmický
odpor rezistoru. Pokud je ω.C.R << 1, je přenos napětí přibližně roven jedné, tj. člen RC
nepotlačuje napětí.
Kmitočet, při kterém platí ω.C.R = 1 se nazývá kmitočet zlomu. Dochází k poklesu napětí −3 dB (A = 0,707) a vypočítá se ze vztahu:

Fázový posuv je při tomto kmitočtu roven -45°.

Horní propust (derivační článek RC a RL)

Derivační článek má frekvenční charakteristiku hornopropustného filtru – se zvyšující se frekvencí vstupního napětí výstupní napětí roste. U ideálního derivátoru odpovídá desetinásobnému zvýšení frekvence desetinásobný vrůst amplitudy, sklon jeho logaritmické amplitudové frekvenční charakteristiky tedy je +20 dB/dek.

Pro derivační člen RC lze absolutní hodnotu přenosu napětí vyjádřit vztahem:

Kmitočet, při kterém dochází k poklesu napětí −3 dB (AU = 0,707), se označuje jako kmitočet zlomu a vypočítá se ze vztahu:

Fázový posuv je při tomto kmitočtu roven -45°.

Pásmové propusti

Pásmová propust – Wienův článek je kombinací dolní a horní propusti. Hodnoty součástek jsou spočítány pro jeden zlomový kmitočet fz. Wienův článek propustí signál zeslabený o 1/3 ze vstupního signálu. Používá se například v generátorech sinusového napětí.

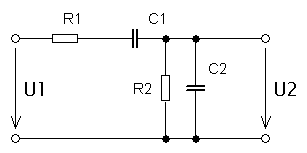
Napěťový přenos je dán vztahem:

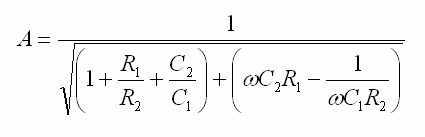
Maximum přenosu je při kritické frekvenci f₀.

Nejčastěji se používají články ve kterých je R1=R2=R a C2=C1=C, potom platí:

Pásmová pasivní zádrž

Souměrný dvojitý článek T je v praxi používán nejčastěji.

Výpočet kritické frekvence a přenosu:

Při n=0,5 článek zcela potlačuje napětí kritické frekvence a pro přenos v závislosti na poměrném rozladění platí: